之前会环形打印矩阵，遇到了一个斜着打印矩阵的问题，觉得蛮有意思。

思考、算法和实现如下

一、思考
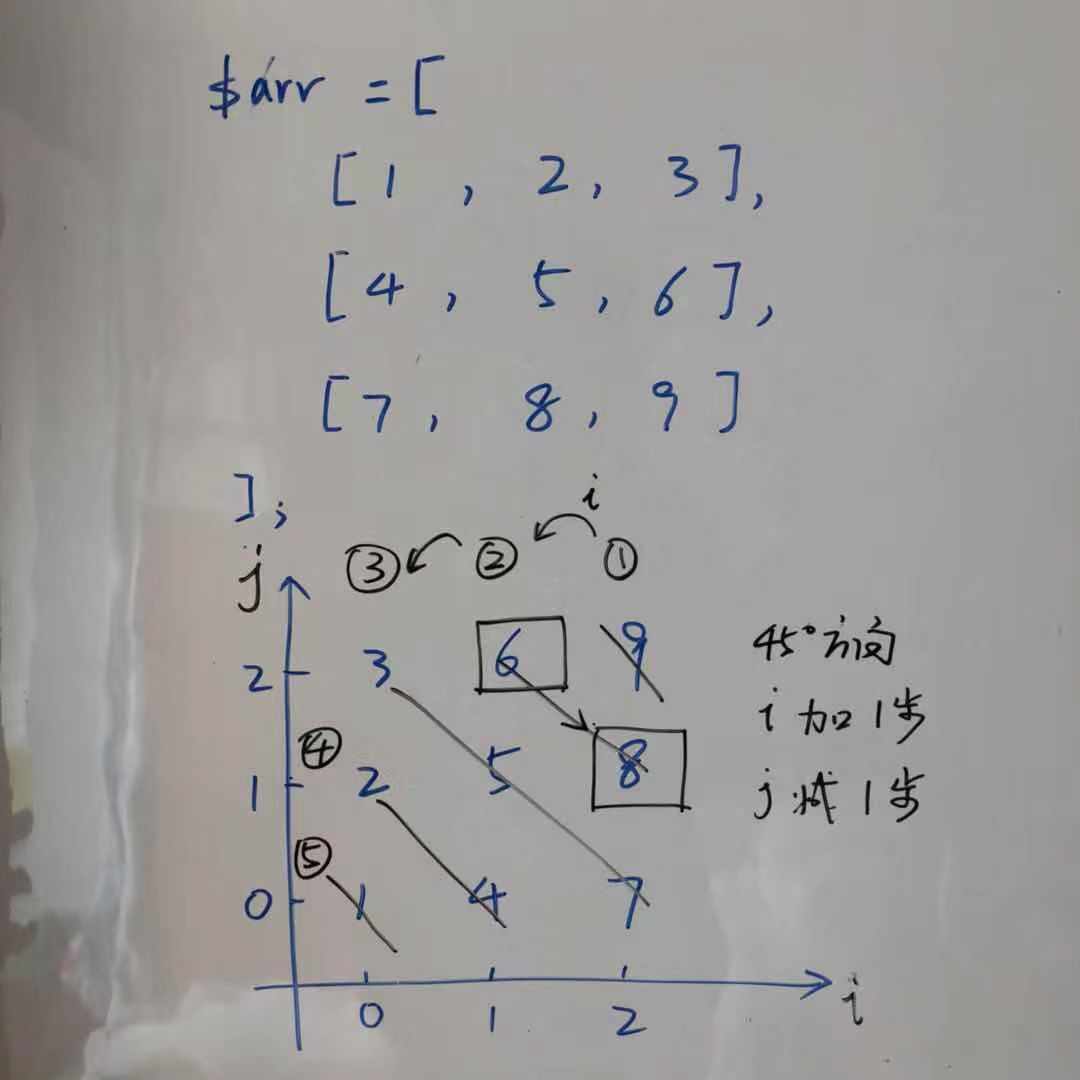
0、在纸上画出一个矩阵，放到坐标轴中，进行分析。【直观上放在坐标轴第4象限好理解，其实放在第一象限有利于分析】

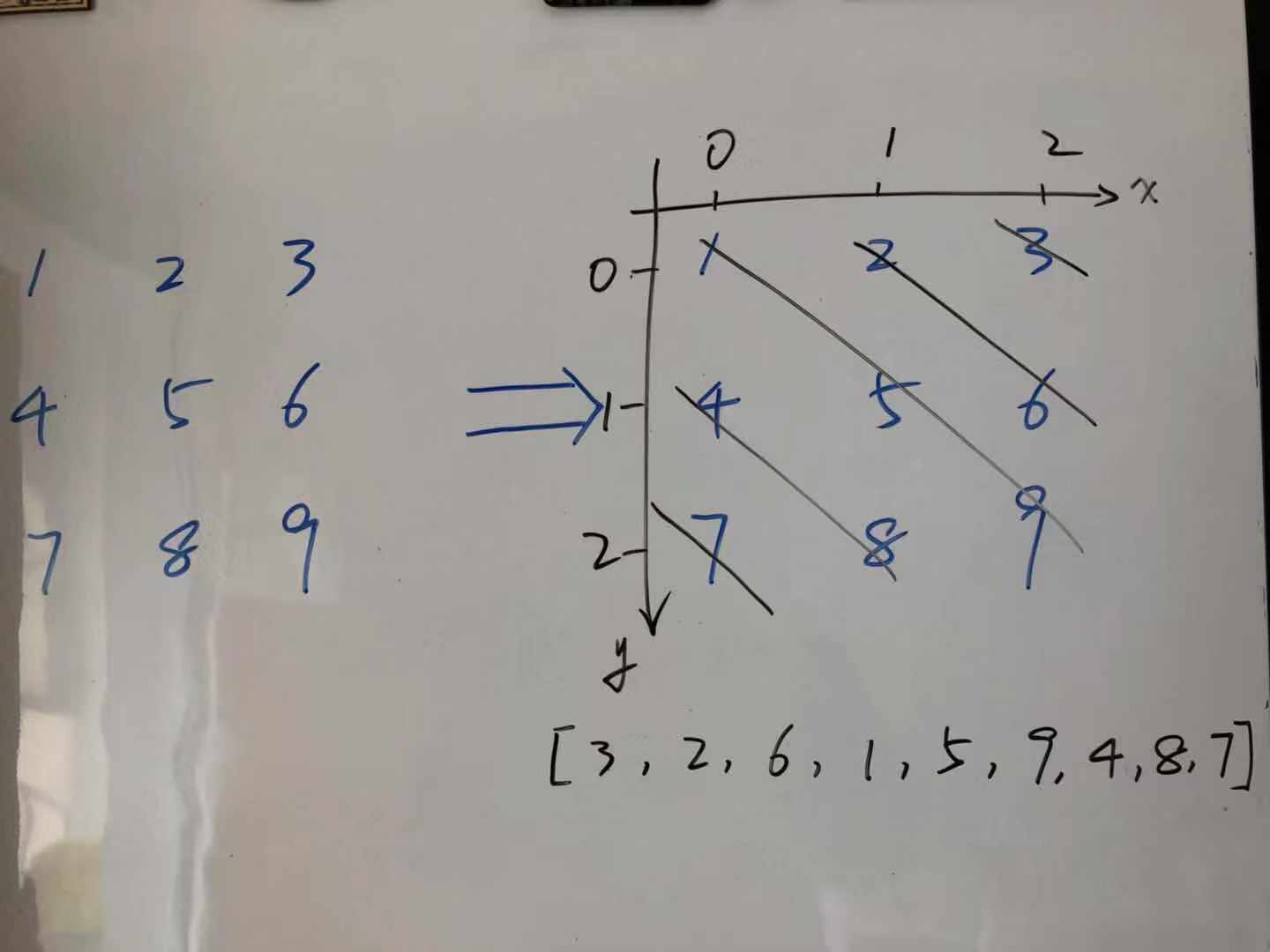
1、很容易发现有2中倾斜方式(正斜，反斜)，每种倾斜方式有2个打印方向。共用四种打印方式，明确一种就行了。下文记录的打印方式是反斜，从右上角往左下角打印。

2、先考虑特殊的情况矩阵行和列相等的情况(m = n = 3)。
算法：

2.0、先打印对角线右上部分。
2.1、定义变量i = m - 1标示第一斜行，沿着斜行打印行上每一个数字，即每打印一个数字往45度角方向移动一步，定义变量j标示移动步数。计算出当前斜线上每个数的下标，打印出来。注意下标越界检查。
2.2、i逐步减1，移动到下一行，然后打印整行。
2.3、直到i减少到0，右上部分打印完成。
2.4、打印对角线左下部分。
2.5、定义变量j = n - 2标示第一斜行，沿着斜行打印行上每一个数字，即每打印一个数字往45度角方向移动一步，定义变量i标示移动步数。计算出当前斜线上每个数的下标，打印出来。注意下标越界检查。
2.6、j逐步减1，移动到下一行，然后打印整行。
2.7、直到j减少到0，右上部分打印完成。

3、在考虑m != n的情况即可。

二、实现(PHP代码)
说明：
0、实现的时候注意定义的数组，最好画在纸上。【可能跟你想的方位不一样】

1、先实现矩阵m = n的情况

function printMatrixSlash($matrix)
{
    $len = count($matrix);
    $res = [];
    // 右上
    for ($i = $len - 1; $i >= 0; $i--) {
        for ($j = 0; $j < $len; $j++) {
            if (($i + $j) < $len) {
                // echo $matrix[$i + $j][$len - 1 - $j], PHP_EOL;
                $res[] = $matrix[$i + $j][$len - 1 - $j];
            }
        }
    }

    // 左下
    for ($j = $len - 2; $j >= 0; $j--) {
        for ($i = 0; $i < $len; $i++) {
            if ($i <= $j) {
                // echo $matrix[$i][$j - $i], PHP_EOL;
                $res[] = $matrix[$i][$j - $i];
            }
        }
    }

    return $res;
}

$arr1 = [
    0 => [1, 2, 3],
    1 => [4, 5, 6],
    2 => [7, 8, 9],
];

$res = printMatrixSlash($arr1);
echo implode(',', $res), PHP_EOL;

以上输出：

9,6,8,3,5,7,2,4,1

2、实现m != n的情况

function printMatrixSlashMN($matrix)
{
    $m = count($matrix);
    $n = count($matrix[0]);
    $res = [];
    // 右上
    for ($i = $m - 1; $i >= 0; $i--) {
        for ($j = 0; $j < $n; $j++) {
            if (($i + $j) < $m) {
                // echo $matrix[$i + $j][$n - 1 - $j], PHP_EOL;
                $res[] = $matrix[$i + $j][$n - 1 - $j];
            }
        }
    }

    // 左下
    for ($j = $n - 2; $j >= 0; $j--) {
        for ($i = 0; $i < $m; $i++) {
            if ($i <= $j) {
                // echo $matrix[$i][$j - $i] , PHP_EOL;
                $res[] = $matrix[$i][$j - $i];
            }
        }
    }

    return $res;
}

$res1 = printMatrixSlashMN($arr1);
$res2 = printMatrixSlashMN($arr2);
$res3 = printMatrixSlashMN($arr3);
echo implode(',', $res1), PHP_EOL;
echo implode(',', $res2), PHP_EOL;
echo implode(',', $res3), PHP_EOL;

以上输出:

9,6,8,3,5,7,2,4,1
6,3,5,2,4,1
8,6,7,4,5,2,3,1

三、总结
0、没有思路的时候记得动手画图。
1、打印每斜行数据的时候，要基于当前节点，计算下一个节点的下标。