一、什么是堆
堆是一种数据结构,特殊的树形数据结构。常见的堆有二叉堆、二项式堆、斐波拉契堆等。
堆这种数据结构主要用来实现两个功能:堆排序和优先队列。
PHP SPL中有堆这种数据结构(SplHeap),及优先队列(SplPriorityQueue)。
二、细说二叉堆
这里细说的堆排序使用的是二叉堆,那么二叉堆是什么样的呢
二叉堆是一颗完全二叉树(维基百科提到还有可能是近似完全二叉树,很不理解),节点和双亲节点维持着固定的关系,要么节点的值都大于双亲节点,要么节点的值都小于双亲节点,并且每个节点的左右子树都是二叉堆。【完全二叉树及堆的图,可参考知乎专栏,传送门】
特点:
0、节点都大于双亲节点的二叉堆叫大顶堆。
1、节点都小于双亲节点的二叉堆叫小顶堆。
2、二叉堆一般用一维数组来存储。
3、二叉堆一个节点的左右孩子没有顺序。
4、有n个元素的二叉堆,最后一个非叶节点为n/2 -1
三、二叉堆的树形结构
把如下的一个一维数组还原为二叉堆的树形结构
$arr = [8, 10, 6, 2, 9, 15, 1, 60, 27];
树形结构如下:
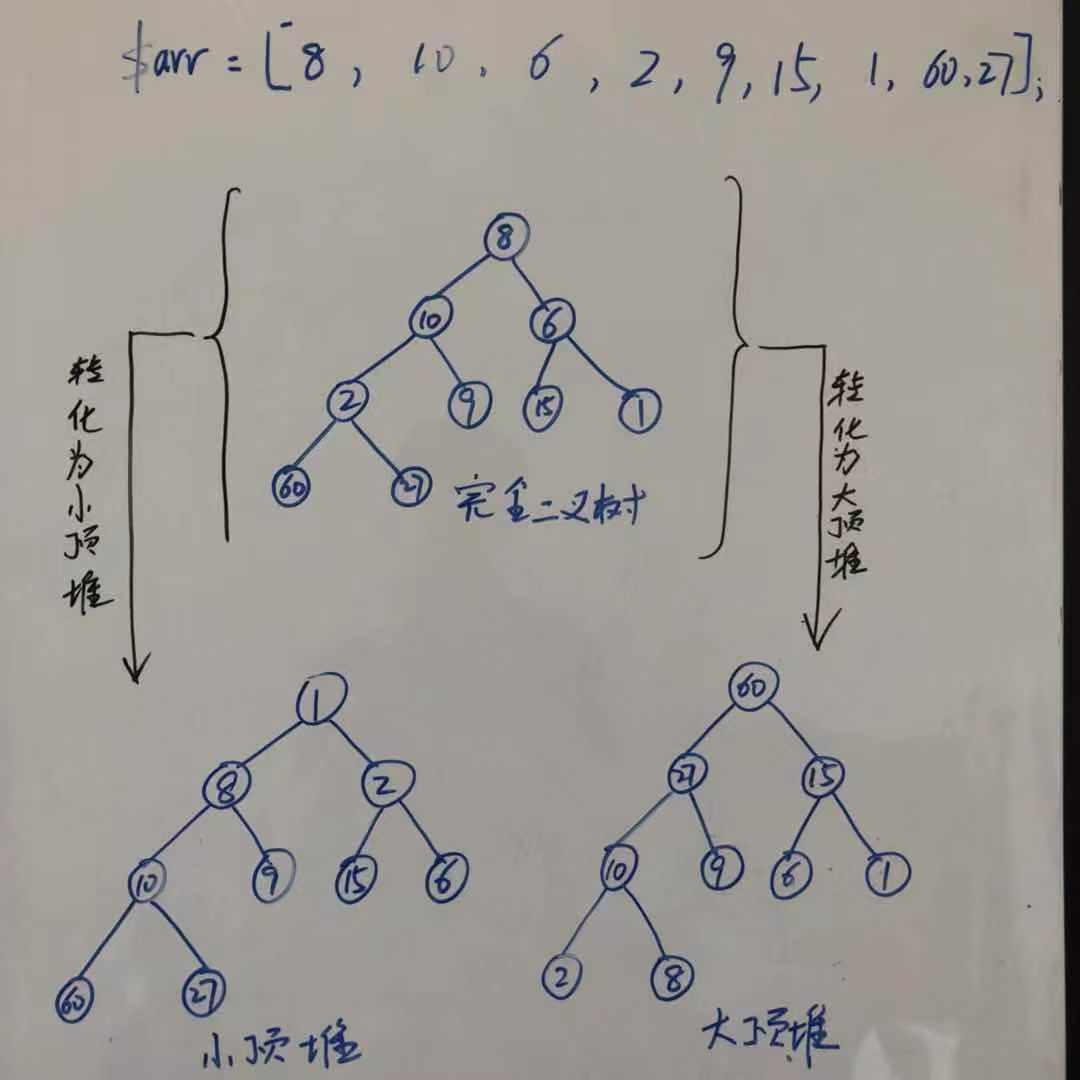
图上展示了原始的完全二叉树,以及转化后的大小顶堆的树形结构。如何转化后面会有步骤介绍,不用迷茫。
四、堆排序过程
这里以小顶堆为例
思路:
把一个有n个无序序列(一维数组)转化为小顶堆,此时堆顶元素就是最小的元素,用堆顶元素和数组最后一个元素交换,最后一个元素就排好序了,剩余的n-1个元素按照这个规律,先构建小顶堆,再交换,最终达到有序。【跟选择排序是不是有点像,其实就是选择排序的升级版】
算法: 0、先把n个元素构建成小顶堆。 1、将根节点与最后一个元素交换位置。[将最小元素沉到数组末尾] 2、将剩下n-1个元素构建成小顶堆。[交换后可能不在是小顶堆] 3、重复1-2直到数据全部有序。[降序]
介绍具体的实现之前,我们先来看看如果构建一个小顶堆,也就是上图中原始完全二叉树转为小顶堆的过程,搞清楚这一步,堆排序基本搞清楚了一半。
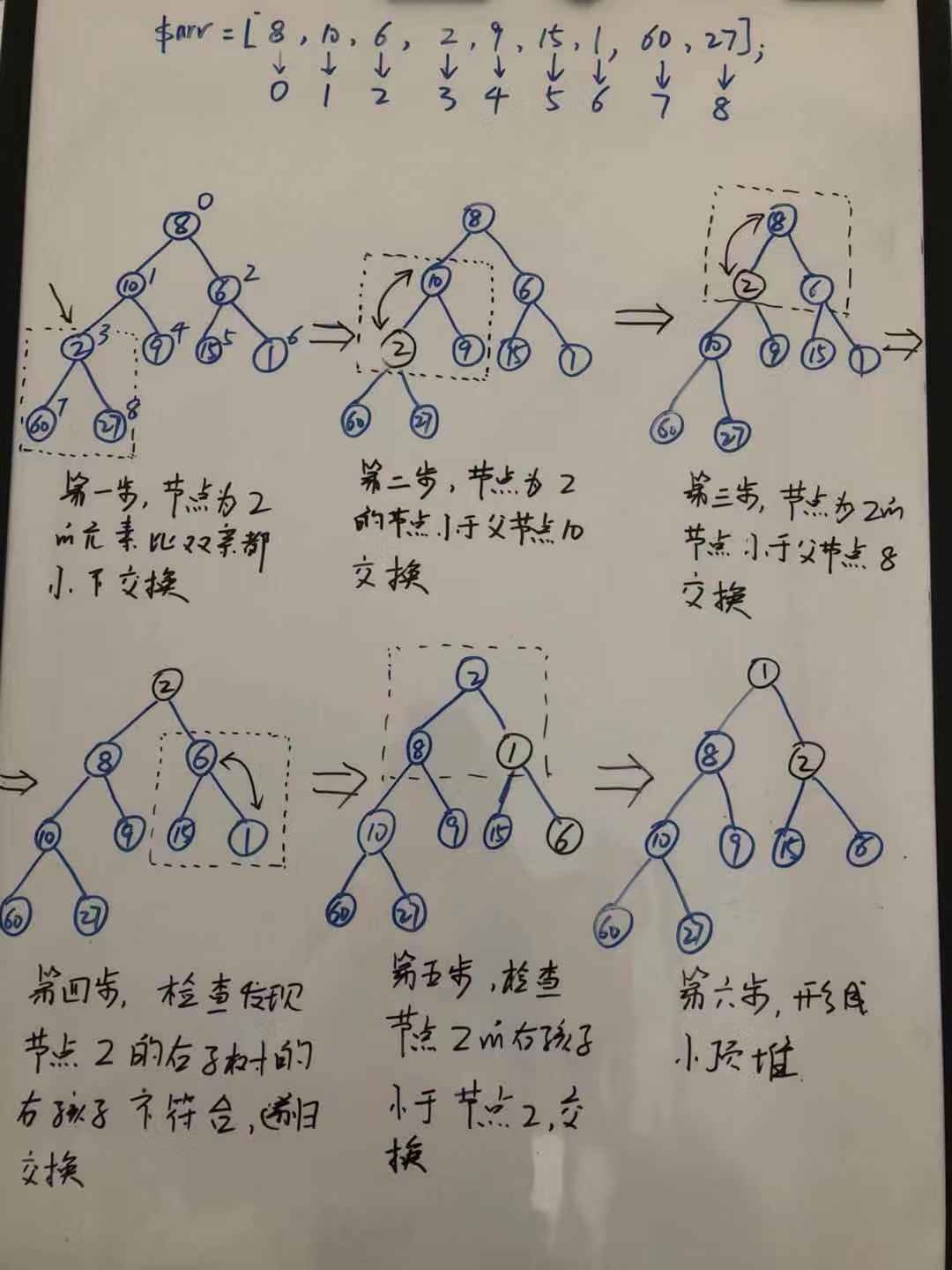
PHP代码实现构造小顶堆如下:
/**
* 构造小顶堆
*
* @param array $heap 数组
* @param int $len 数组长度
*
* @return array
*/
public static function buildMinHeap(&$heap, $len)
{
// 最后一个非叶节点下标
$last_index = floor($len / 2) - 1;
for ($i = $last_index; $i >= 0; $i--) {
// 如果有左孩子,并且左孩子大于当前节点,交换
$lchild_index = 2 * $i + 1;
if ($lchild_index < $len && $heap[$lchild_index] < $heap[$i]) {
self::swap($heap, $lchild_index, $i);
// 左孩子的左孩子下标
$llchild_index = 2 * $lchild_index + 1;
// 左孩子的右孩子下标
$rlchild_index = 2 * $lchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为小顶堆,或者当前节点的右子树存在,则调整为小顶堆
if (($llchild_index < $len && $heap[$llchild_index] < $heap[$lchild_index]) OR ($rlchild_index < $len && $heap[$rlchild_index] < $heap[$lchild_index])) {
self::buildMinHeap($heap, $len);
}
}
// 如果有右孩子,并且右孩子大于当前节点,交换
$rchild_index = 2 * $i + 2;
if ($rchild_index < $len && $heap[$rchild_index] < $heap[$i]) {
self::swap($heap, $rchild_index, $i);
// 右孩子的左孩子下标
$lrchild_index = 2 * $rchild_index + 1;
// 右孩子的右孩子下标
$rrchild_index = 2 * $rchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为小顶堆,或者当前节点的右子树存在,则调整为小顶堆
if (($lrchild_index < $len && $heap[$lrchild_index] < $heap[$rchild_index]) OR ($rrchild_index < $len && $heap[$rrchild_index] < $heap[$rchild_index])) {
self::buildMinHeap($heap, $len);
}
}
}
}
完整的代码实现如下,包含小顶堆排序和大顶堆排序
五、小顶堆排序PHP实现
/*
*
* 小顶堆排序
* 算法:
* 0、先把n个元素构建成小顶堆。
* 1、将根节点与最后一个元素交换位置。[将最小元素沉到数组末尾]
* 2、将剩下n-1个元素构建成小顶堆。[交换后可能不在是小顶堆]
* 3、重复1-2直到数据全部有序。[降序]
*/
class Heapsort
{
/**
* 构造小顶堆
*
* @param array $heap 数组
* @param int $len 数组长度
*
* @return array
*/
public static function buildMinHeap(&$heap, $len)
{
// 最后一个非叶节点下标
$last_index = floor($len / 2) - 1;
for ($i = $last_index; $i >= 0; $i--) {
// 如果有左孩子,并且左孩子大于当前节点,交换
$lchild_index = 2 * $i + 1;
if ($lchild_index < $len && $heap[$lchild_index] < $heap[$i]) {
self::swap($heap, $lchild_index, $i);
// 左孩子的左孩子下标
$llchild_index = 2 * $lchild_index + 1;
// 左孩子的右孩子下标
$rlchild_index = 2 * $lchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为小顶堆,或者当前节点的右子树存在,则调整为小顶堆
if (($llchild_index < $len && $heap[$llchild_index] < $heap[$lchild_index]) OR ($rlchild_index < $len && $heap[$rlchild_index] < $heap[$lchild_index])) {
self::buildMinHeap($heap, $len);
}
}
// 如果有右孩子,并且右孩子大于当前节点,交换
$rchild_index = 2 * $i + 2;
if ($rchild_index < $len && $heap[$rchild_index] < $heap[$i]) {
self::swap($heap, $rchild_index, $i);
// 右孩子的左孩子下标
$lrchild_index = 2 * $rchild_index + 1;
// 右孩子的右孩子下标
$rrchild_index = 2 * $rchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为小顶堆,或者当前节点的右子树存在,则调整为小顶堆
if (($lrchild_index < $len && $heap[$lrchild_index] < $heap[$rchild_index]) OR ($rrchild_index < $len && $heap[$rrchild_index] < $heap[$rchild_index])) {
self::buildMinHeap($heap, $len);
}
}
}
}
/**
* 交换数组中两个元素
*
* @param array $arr 数组
* @param int|string $key1 数组中元素索引
* @param int|string $key2 数组中元素索引
*
* @return array
*/
public static function swap(&$arr, $key1, $key2)
{
$tmp = $arr[$key1];
$arr[$key1] = $arr[$key2];
$arr[$key2] = $tmp;
}
/**
* 小顶堆排序
*
* @param array $heap 数组
* @param int $len 数组长度
*
* @return array
*/
public static function minHeapSort($arr, $len)
{
for ($i = $len; $i > 0; $i--) {
Heapsort::buildMinHeap($arr, $i);
Heapsort::swap($arr, 0, $i - 1);
}
return $arr;
}
}
// test case
$arr = [8, 10, 6, 2, 9, 15, 1, 60, 27];
$len = count($arr);
// 小顶堆排序
$min_heap_res = Heapsort::minHeapSort($arr, $len);
var_dump($min_heap_res);
// the end of the script
六、大顶堆排序PHP实现
/*
* 堆排序
* 大顶堆排序
* 算法:
* 0、先把n个元素构建成大顶堆。
* 1、将根节点与最后一个元素交换位置。[将最大元素沉到数组末尾]
* 2、将剩下n-1个元素构建成大顶堆。[交换后可能不在是大顶堆]
* 3、重复1-2直到数据全部有序。[升序]
*
*/
class Heapsort
{
/**
* 构造大顶堆
*
* @param array $heap 数组
* @param int $len 数组长度
*
* @return array
*/
public static function buildMaxHeap(&$heap, $len)
{
// 最后一个非叶节点下标
$last_index = floor($len / 2) - 1;
for ($i = $last_index; $i >= 0; $i--) {
// 如果有左孩子,并且左孩子大于当前节点,交换
$lchild_index = 2 * $i + 1;
if ($lchild_index < $len && $heap[$lchild_index] > $heap[$i]) {
self::swap($heap, $lchild_index, $i);
// 左孩子的左孩子下标
$llchild_index = 2 * $lchild_index + 1;
// 左孩子的右孩子下标
$rlchild_index = 2 * $lchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为大顶堆,或者当前节点的右子树存在,则调整为大顶堆
if (($llchild_index < $len && $heap[$llchild_index] > $heap[$lchild_index]) OR ($rlchild_index < $len && $heap[$rlchild_index] > $heap[$lchild_index])) {
self::buildMaxHeap($heap, $len);
}
}
// 如果有右孩子,并且右孩子大于当前节点,交换
$rchild_index = 2 * $i + 2;
if ($rchild_index < $len && $heap[$rchild_index] > $heap[$i]) {
self::swap($heap, $rchild_index, $i);
// 右孩子的左孩子下标
$lrchild_index = 2 * $rchild_index + 1;
// 右孩子的右孩子下标
$rrchild_index = 2 * $rchild_index + 2;
// 递归调用: 当前节点的左子树存在,则调整为大顶堆,或者当前节点的右子树存在,则调整为大顶堆
if (($lrchild_index < $len && $heap[$lrchild_index] > $heap[$rchild_index]) OR ($rrchild_index < $len && $heap[$rrchild_index] > $heap[$rchild_index])) {
self::buildMaxHeap($heap, $len);
}
}
}
}
/**
* 交换数组中两个元素
*
* @param array $arr 数组
* @param int|string $key1 数组中元素索引
* @param int|string $key2 数组中元素索引
*
* @return array
*/
public static function swap(&$arr, $key1, $key2)
{
$tmp = $arr[$key1];
$arr[$key1] = $arr[$key2];
$arr[$key2] = $tmp;
}
/**
* 大顶堆排序
*
* @param array $heap 数组
* @param int $len 数组长度
*
* @return array
*/
public static function maxHeapSort($arr, $len)
{
for ($i = $len; $i > 0; $i--) {
Heapsort::buildMaxHeap($arr, $i);
Heapsort::swap($arr, 0, $i - 1);
}
return $arr;
}
}
// test case
$arr = [8, 10, 6, 2, 9, 15, 1, 60, 27];
$len = count($arr);
// 大定堆排序
$max_heap_res = Heapsort::maxHeapSort($arr, $len);
var_dump($max_heap_res);
// the end of the script
七、算法复杂度分析
0、建堆时间复杂度 O(n)
1、建堆空间复杂度 O(n)
2、堆排序时间复杂度 O(nlog n)
3、堆排序空间复杂度 O(1)
4、堆插入元素时间复杂度 O(log n)
5、堆删除元素时间复杂度 O(log n)
八、应用
0、优先级队列:合并有序小文件
1、优先级队列:高性能定时器
2、求Top K
3、求中位数
4、leetcode#347 前K个高频元素
详细解读可见博文: 堆的应用:如何快速获取到Top 10最热门的搜索关键词
九、思考
画图的过程中在思考,代码中每次都需要递归,实现简单,这种实现时间复杂度能达到O(nlog n)么?
另外网上流传很广的这篇文章,PHP实现堆排序,测试发现,构建调用构建堆的方法后构建的根本不是小顶堆,交换后没有维护左右子树堆的状态,怎么看都像是披着选择排序算法的堆排序
